Keywords: non-local ductile damage modelling, coupled multifield problems, element technology, stabilisation.

The modelling of fracture in ductile metals as a result of damage is often based on the micromechanical model of Gurson [1] for the growth of a single void in an ideal elastoplastic matrix. In order to account for the effects of void nucleation and coalescence, and so to obtain better agreement between the model, experimental results and numerical simulations for ductile failure and crack propagation, the original local Gurson model, and in particular the Gurson yield function, was modified and extended into a local semi-phenomenological form in [2,3,4]. As has been demonstrated in many other contexts, initially homogeneous solutions to the boundary-value problem based on such local models (e.g. which can soften) become unstable with increasing loading, resulting in a transition to localised deformation, e.g. in the form of shear bands. Finite-element-based simulations of this process utilising purely local models of this type have demonstrated that simulation results such as the load-displacement response or the width of shear bands depend strongly on the properties of the corresponding finite-element mesh. In order to deal with this, a number of non-local extensions to ductile damage modelling have been proposed and implemented (e.g. [5,6,7,8,9]). The purpose of this work is the algorithmic and finite-element formulation of a non-local extension of existing Gurson-based modelling of isotropic ductile damage and failure. The model itself is based on the premise that void coalescence results not only in accelerated damage development, but also in damage delocalisation (i.e. via interaction between neighbouring Gurson representative volume elements). To this end, we follow the approach of Needleman and Tvergaard [3], who replaced the Gurson void volume fraction 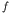with a (local) effective damage parameter 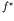in the Gurson yield condition to account for the effect of void coalescence on the material behaviour. In the current case, the role of 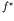is taken over and generalised by an effective continuum damage field . A field relation for is formulated here in the framework of continuum thermodynamics. Analogous to temperature, represents then an additional continuum degree-of-freedom, resulting in a coupled deformation-damage field model. This coupled damage-deformation model is then formulated algorithmically via backward-Euler integration and consistent linearisation. In order to utilize the model in metal forming and other simulations where large bending can occur, the element formulation for the mechanical degrees-of-freedom is carried out using the enhanced approach (e.g. [10]). Because this approach suffers from the problem of hourglassing, and in order to work with one-Gauss-point elements, the element formulation for both the mechanical and damage degrees-of-freedom is further based on the use of advanced stabilisation techniques developed in [11] for coupled temperature-deformation problems.

1

A. L. Gurson, "Continuum theory of ductile rupture by void nucleation and growth: Part I-yield criteria and flow rules for porous ductile media", Journal of Engineering Materials and Technology, 99, 2-15, 1977.

2

C. C. Chu, A. Needleman, "Void nucleation effects in biaxially stretched sheets", Journal of Engineering Materials and Technology, 102, 249-256, 1980.

3

A. Needleman, V. Tvergaard, "An analysis of ductile rupture in notched bars", Journal of the Mechanics and Physics of Solids 32, 461-490, 1984. doi:10.1016/0022-5096(84)90031-0

4

J. Koplic, A. Needleman, "Void growth and coalescence in porous plastic solids", International Joural of Solids and Structures, 24, 835-853, 1988. doi:10.1016/0020-7683(88)90051-0

5

V. Tvergaard, A. Needleman, "Effects of non-local damage in porous plastic solids", International Joural of Solids and Structures, 32, 1063-1077, 1995. doi:10.1016/0020-7683(94)00185-Y

6

S. Ramaswamy, N. Aravas, "Finite element implementation of gradient plasticity models. Part I: Gradient-dependent yield functions", Computer Methods in Applied Mechanics and Engineering, 163, 11-32, 1998a. doi:10.1016/S0045-7825(98)00028-0

7

S. Ramaswamy, N. Aravas, "Finite element implementation of gradient plasticity models. Part II: Gradient-dependent evolutions equations", Computer Methods in Applied Mechanics and Engineering, 163, 33-53, 1998b. doi:10.1016/S0045-7825(98)00027-9

8

M. G. D. Geers, R. L. J. M. Ubachs, R. A. B. Engelen, "Strongly non-local gradient-enhanced finite strain elastoplasticity", International Journal for Numerical Methods in Engineering, 49, 1-53, 2000. doi:10.1002/nme.654

9

F. Reusch, B. Svendsen, D. Klingbeil, "Local and non-local Gurson-based ductile damage and failure modelling at large deformation", European Journal of Mechanics A/Solids, 22, 779-792, 2003. doi:10.1016/S0997-7538(03)00070-6

10

J. C. Simo, M. S. Rifai, "A class of mixed assumed strain methods and the method of incompatible modes", International Journal for Numerical Methods in Engineering 29, 1595-1638, 1990. doi:10.1002/nme.1620290802

11

S. Reese, "On a consistent hourglass stabilization technique to treat large inelastic deformations and thermo-mechanical coupling in plane strain problems", International Journal for Numerical Methods in Engineering, 57, 1095-1127, 2003. doi:10.1002/nme.719

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)