
Computational & Technology Resources
an online resource for computational,
engineering & technology publications
engineering & technology publications
Civil-Comp Proceedings
ISSN 1759-3433
ISSN 1759-3433
CCP: 81
PROCEEDINGS OF THE TENTH INTERNATIONAL CONFERENCE ON CIVIL, STRUCTURAL AND ENVIRONMENTAL ENGINEERING COMPUTING
PROCEEDINGS OF THE TENTH INTERNATIONAL CONFERENCE ON CIVIL, STRUCTURAL AND ENVIRONMENTAL ENGINEERING COMPUTING
Edited by: B.H.V. Topping
Paper 126
Explicit Formulations for Reliability-Based Optimal Plastic Design Problems
K. Marti
Aero-Space Engineering and Technology, Federal Armed Forces University Munich, Neubiberg/Munich, Germany
Full Bibliographic Reference for this paper
K. Marti, "Explicit Formulations for Reliability-Based Optimal Plastic Design Problems", in B.H.V. Topping, (Editor), "Proceedings of the Tenth International Conference on Civil, Structural and Environmental Engineering Computing", Civil-Comp Press, Stirlingshire, UK, Paper 126, 2005. doi:10.4203/ccp.81.126
Keywords: optimal plastic design under stochastic uncertainty, FORM, explicit representation of the projection problem, explicit formulations of (RBDO) problems.
Summary
Problems from optimal plastic design are based on the convex or piecewise linear yield criterion and the linear equilibrium equation for the generic stress (state) vector 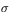 . Having taken into account, in practice, stochastic variations of the vector
. Having taken into account, in practice, stochastic variations of the vector
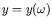 of the model parameters, e.g. yield stresses, external loadings, cost coefficients, etc., the basic stochastic optimal plastic design problem is replaced - in order to get robust optimal designs - by a deterministic substitute problem with probabilistic constraints. Survival/failure of an elastic-plastic structure is described with the new limit state function based on the static limit theorem for elastic-plastic structures. This function
of the model parameters, e.g. yield stresses, external loadings, cost coefficients, etc., the basic stochastic optimal plastic design problem is replaced - in order to get robust optimal designs - by a deterministic substitute problem with probabilistic constraints. Survival/failure of an elastic-plastic structure is described with the new limit state function based on the static limit theorem for elastic-plastic structures. This function
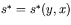 can be represented explicitly by the minimum value function of a convex or linear program, related to the basic survival conditions, depending on the parameter vector
can be represented explicitly by the minimum value function of a convex or linear program, related to the basic survival conditions, depending on the parameter vector 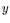 and the design vector
and the design vector 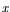 . Hence, the probability of survival can be represented [1] by
. Hence, the probability of survival can be represented [1] by
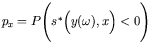 . Using (FORM), the probability of survival is approximated then by the formula
. Using (FORM), the probability of survival is approximated then by the formula
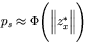 , where
, where
 denotes the length of a so-called beta- or "design" point
denotes the length of a so-called beta- or "design" point 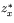 . In general, the computation of this projection
. In general, the computation of this projection 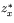 of the origin 0 to the failure domain is very difficult. However, in the present case, due to the new limit state function
of the origin 0 to the failure domain is very difficult. However, in the present case, due to the new limit state function
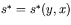 , an explicit representation of the projection problem for the calculation of the design point
, an explicit representation of the projection problem for the calculation of the design point 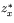 is available. Consequently, also the necessary optimality conditions for the projection problem are available explicitly. For the basic reliability-based design optimization (RBDO) problem [2]
is available. Consequently, also the necessary optimality conditions for the projection problem are available explicitly. For the basic reliability-based design optimization (RBDO) problem [2]
where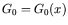 is the initial cost function,
is the initial cost function, 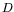 denotes the domain of feasible designs
denotes the domain of feasible designs 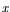 , and
, and 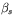 is a given reliability level, a standard solution technique is the two-level method with two nested optimization problems. However, based on the above mentioned explicit representation of the projection problem, two explicit representations of the (RBDO) problem are obtained:
is a given reliability level, a standard solution technique is the two-level method with two nested optimization problems. However, based on the above mentioned explicit representation of the projection problem, two explicit representations of the (RBDO) problem are obtained:
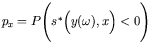 . Using (FORM), the probability of survival is approximated then by the formula
. Using (FORM), the probability of survival is approximated then by the formula
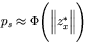 , where
, where
where
- i)
- Using the explicit necessary conditions of the projection problem:
Since the projection problem is given explicitly, also the corresponding necessary (sufficient) optimality conditions can be stated explicitly. Hence, in the present case, the optimality condition in the above (RBDO) problem is replaced by the necessary optimality conditions for
in the above (RBDO) problem is replaced by the necessary optimality conditions for 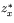 derived from the projection problem. Numerical results show that somewhat higher initial
derived from the projection problem. Numerical results show that somewhat higher initial  -values must be chosen in some cases for guaranteeing the desired reliability level
-values must be chosen in some cases for guaranteeing the desired reliability level 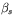 .
.
- ii)
- Relaxation methods:
In many cases the reliability condition can be represented bywhere for all
for all 
 is a given set of dual variables
is a given set of dual variables  , and
, and
 is the projection of the origin in the
parameter space onto a given (simple) surface in
is the projection of the origin in the
parameter space onto a given (simple) surface in  -space depending on
-space depending on  , where this projection can be determined
explicitly. Hence, a semi-infinite optimization problem is obtained in this case. This problem can be solved
then by known approximation techniques reducing e.g. the problem to a finite dimensional parameter optimization problem
again.
, where this projection can be determined
explicitly. Hence, a semi-infinite optimization problem is obtained in this case. This problem can be solved
then by known approximation techniques reducing e.g. the problem to a finite dimensional parameter optimization problem
again.
References
- 1
- K. Marti, "Plastic Sturcutral Analysis under Stochastic Uncertainty", MCMDS, 9, Issue 3, 303-325, 2003. doi:10.1076/mcmd.9.3.303.24149
- 2
- N. Kushel and R. Rackwitz, "Two basic problems in reliability-based structural optimization", Mathematical Methods of Operational Research, 46, 309-333, 1997. doi:10.1007/BF01194859
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)