
Computational & Technology Resources
an online resource for computational,
engineering & technology publications
engineering & technology publications
Civil-Comp Proceedings
ISSN 1759-3433
ISSN 1759-3433
CCP: 81
PROCEEDINGS OF THE TENTH INTERNATIONAL CONFERENCE ON CIVIL, STRUCTURAL AND ENVIRONMENTAL ENGINEERING COMPUTING
PROCEEDINGS OF THE TENTH INTERNATIONAL CONFERENCE ON CIVIL, STRUCTURAL AND ENVIRONMENTAL ENGINEERING COMPUTING
Edited by: B.H.V. Topping
Paper 87
Preconditioning Shifted Linear Systems arising in a Wind Model
G. Montero, A. Suárez, E. Rodríguez, E. Flórez and M.D. García
University Institute for Intelligent Systems and Numerical Applications in Engineering, Las Palmas de Gran Canaria, Spain
Full Bibliographic Reference for this paper
G. Montero, A. Suárez, E. Rodríguez, E. Flórez, M.D. García, "Preconditioning Shifted Linear Systems arising in a Wind Model", in B.H.V. Topping, (Editor), "Proceedings of the Tenth International Conference on Civil, Structural and Environmental Engineering Computing", Civil-Comp Press, Stirlingshire, UK, Paper 87, 2005. doi:10.4203/ccp.81.87
Keywords: shifted linear systems, preconditioning, preconditioned conjugate gradient, wind modelling, mass consistent models.
Summary
Mass consistent models have been widely use in three-dimensional finite element modelling of wind fields. In general, these problems are defined over regions with complex terrain, therefore a suitable discretization of the zone studied will be necessary. Here, we have used a technique for constructing tetrahedral meshes which is adapted to the terrain orography and have a higher density of nodes near the terrain surface [1]. Moreover some regions may need an additional refinement due, for example, to more accurate approximation in those zones [2]. So, in general, we are going to work with meshes including elements of very different sizes. This fact may affect the conditioning of the linear system of equations that arises in this problem from this type of discretization. The numerical modelling of a wind field using a mass consistent model yields a linear system of equations with symmetric positive definite matrix for each set of wind velocities measured at meteorological stations [3]. Thus a suitable preconditioning technique should be applied for an efficient conjugate gradient iteration. This type of linear system may be written as
 , where
, where
 is related to the so-called stability parameter of the wind model, with
is related to the so-called stability parameter of the wind model, with
 . Two different applications exist where a sequence of these linear systems must be solved. On the one hand, we have applied genetic algorithms for the estimation of
. Two different applications exist where a sequence of these linear systems must be solved. On the one hand, we have applied genetic algorithms for the estimation of
 for each given set of station measures [4,5]. The evaluation of the fitness function, which is in general related to the difference between the observed and computed wind at the stations, leads us to solve a complete wind simulation for each individual of the population. In other words, we have to solve a linear system of equations for each value of
for each given set of station measures [4,5]. The evaluation of the fitness function, which is in general related to the difference between the observed and computed wind at the stations, leads us to solve a complete wind simulation for each individual of the population. In other words, we have to solve a linear system of equations for each value of
 . On the other hand, for a given sequence of the parameter
. On the other hand, for a given sequence of the parameter
 related to each set of measures along a simulation episode, a set of linear systems must be solved for each
related to each set of measures along a simulation episode, a set of linear systems must be solved for each
 . Matrices
. Matrices  and
and  do not change along the process for a given discretisation level. The rest of parameters and the wind measures only affect the vector
do not change along the process for a given discretisation level. The rest of parameters and the wind measures only affect the vector  . There are two extreme strategies for preconditioning such linear systems. On the one hand, we can construct an initial preconditioner which is applied without any modification in the resolution of all the linear systems. The performance of the preconditioner will become worse progressively as the process advances, depending on the great or small variation in the value of
. There are two extreme strategies for preconditioning such linear systems. On the one hand, we can construct an initial preconditioner which is applied without any modification in the resolution of all the linear systems. The performance of the preconditioner will become worse progressively as the process advances, depending on the great or small variation in the value of
 . On the other hand, we can use a different preconditioner for each linear system independently. This strategy would be very expensive and slow. So, the main goal of this work is to develop a preconditioner that can be updated as a function of
. On the other hand, we can use a different preconditioner for each linear system independently. This strategy would be very expensive and slow. So, the main goal of this work is to develop a preconditioner that can be updated as a function of
 . We propose the construction of an intermediate approach that works better than the former strategy and worse than the latter in terms of conjugate gradient iterations, but evidently at a lower computational cost. In the past two approaches have been developed for the preconditioning of shifted linear systems. In the particular case of
. We propose the construction of an intermediate approach that works better than the former strategy and worse than the latter in terms of conjugate gradient iterations, but evidently at a lower computational cost. In the past two approaches have been developed for the preconditioning of shifted linear systems. In the particular case of
 with
with 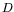 being a diagonal matrix, Meurant [6] proposes a method for updating an incomplete Cholesky factorisation as a function of
being a diagonal matrix, Meurant [6] proposes a method for updating an incomplete Cholesky factorisation as a function of
 . Moreover, Benzi et al [7] propose a technique for updating a preconditioner based on a factorised approximate inverse using
. Moreover, Benzi et al [7] propose a technique for updating a preconditioner based on a factorised approximate inverse using  for the case of
for the case of
 , with
, with  being the unit matrix. The direct generalisation of these procedures to our matrices of the form
being the unit matrix. The direct generalisation of these procedures to our matrices of the form
 leads necessarily to additional simplifications that are less significant when we use the
leads necessarily to additional simplifications that are less significant when we use the  algorithm. Thus in this first study we have followed the same way as Benzi et al. [7]
algorithm. Thus in this first study we have followed the same way as Benzi et al. [7]
References
- 1
- Montenegro R, Montero G, Escobar JM, Rodríguez E, González- Yuste JM. Tetrahedral Mesh Generation for Environmental Problems over Complex Terrain. Lect. Notes in Comp. Sci. 2002;2329:335-344.
- 2
- González-Yuste JM, Montenegro R, Escobar JM, Montero G, Rodríguez E. Local Refinement of 3-D Triangulations Using Object-Oriented Methods. Adv. Engng. Soft. 2004;35:693-702. doi:10.1016/j.advengsoft.2003.07.003
- 3
- Montero G, Montenegro R, Escobar JM. A 3-D Diagnostic Model for Wind Field Adjustment. J. Wind Engng. Ind. Aer. 1998;74-76:249-261. doi:10.1016/S0167-6105(98)00022-1
- 4
- Rodríguez E, Montero G, Montenegro R, Escobar JM, González- Yuste JM, Parameter Estimation in a Three-dimensional Wind Field Model Using Genetic Algorithms. Lect. Notes in Comp. Sci. 2002;2329:950-959.
- 5
- Montero G, Rodríguez E., Montenegro R, Escobar JM, González- Yuste JM. Genetic Algorithms for an Improved Parameter Estimation with Local Refinenent of Tetrahedral Meshes in a Wind Model. Adv. Engng. Soft. 2005;36: 3-10. doi:10.1016/j.advengsoft.2004.03.011
- 6
- Meurant G, On the incomplete Cholesky Decomposition of a class of perturbed matrices. SIAM J. Sci. Comput. 2001;23(2):419-429. doi:10.1137/S1064827500371244
- 7
- Benzi M, Bertaccini D. Approximate Inverse Preconditioning for Shifted Linear Systems. BIT Num. Math. 43(2), 231-244, June 2003. doi:10.1023/A:1026089811044
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)